Introduction

The RANSAC (Random sample and consensus) algorithm is the gold standard in eliminating noise. A while ago, I wrote an article on how the RANSAC algorithm is implemented for finding the model of a straight line in a noisy field of points. The RANSAC algorithm in its original form was developed around finding straight line models when presented with noisy visual data. In this article, I will explore how to implement the RANSAC algorithm a circle model in a noisy set of points. I hope that by the end of this article you will appreciate how beautiful RANSAC is. Sometimes, I get carried away and visualize that human brain is perhaps doing some sort of RANSAC deep inside. Enough!

Consider the data points below

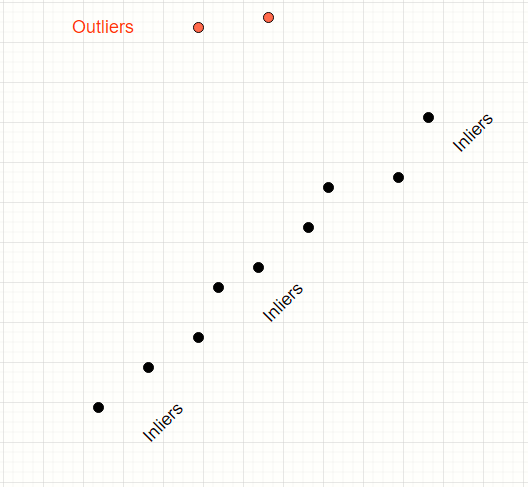
We have a mix of inliers (black) and outliers (red). We want to find the model of the straight line which fits the inliers


The line which fits the data - as perceived by the human eye

The human mind can easily eliminate the outliers.


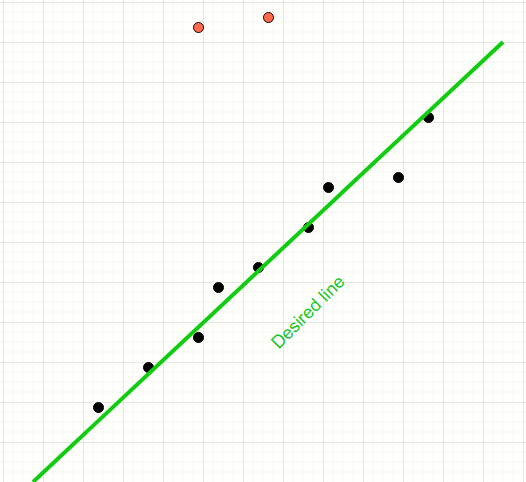
The line which fits the data - computed by the least squares algorithm

The Least Squares method will consider all the points with equal importance. We can clearly see that the resulting line is visibly skewed towards the outliers.


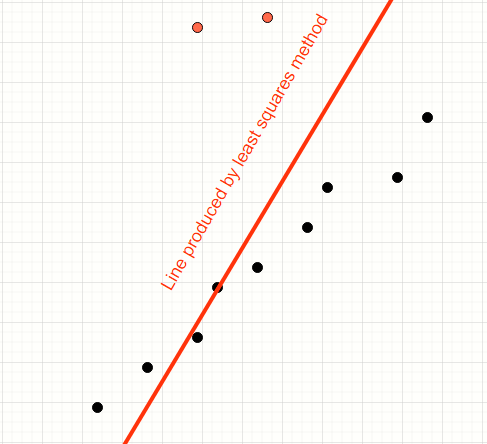
The example shown above exhibits how noise can impact the outcome of the least squares fitting algorithm. The human mind can easily spot the outlier, but the least squares algorithm cannot. This is where RANSAC steps in. RANSAC is a simple voting based algorithm that iteratively samples the population of points and find the subset of those lines which appear to conform.

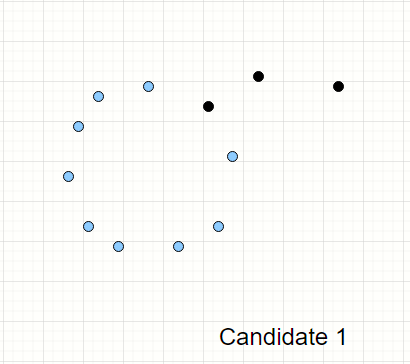
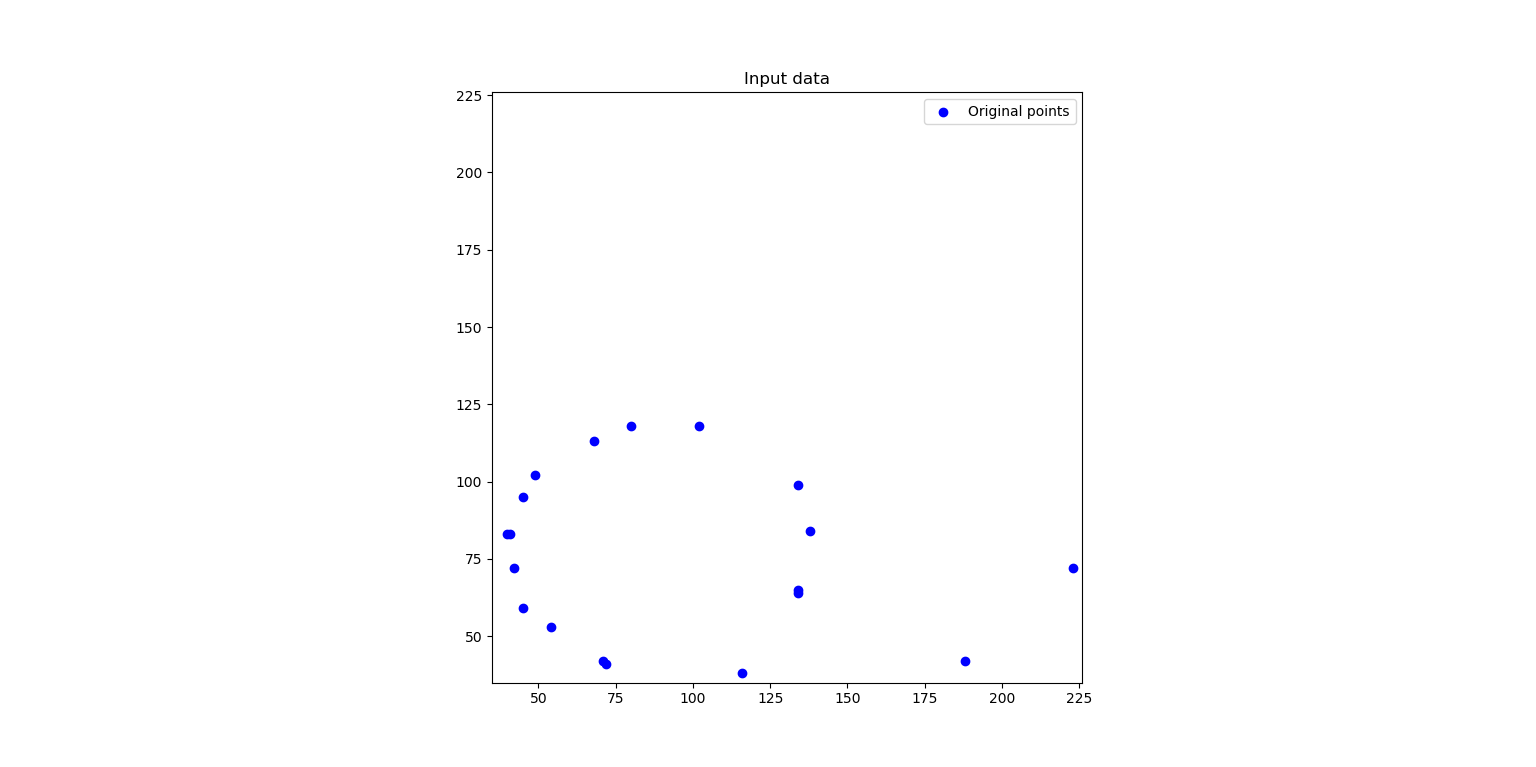
RANSAC for circles - what problem does it solve?

Consider the points shown below. It is not difficult to spot there is a nice circle that can be traced out of the points only if we exclude the 2 noisy points on the far right of the visual.

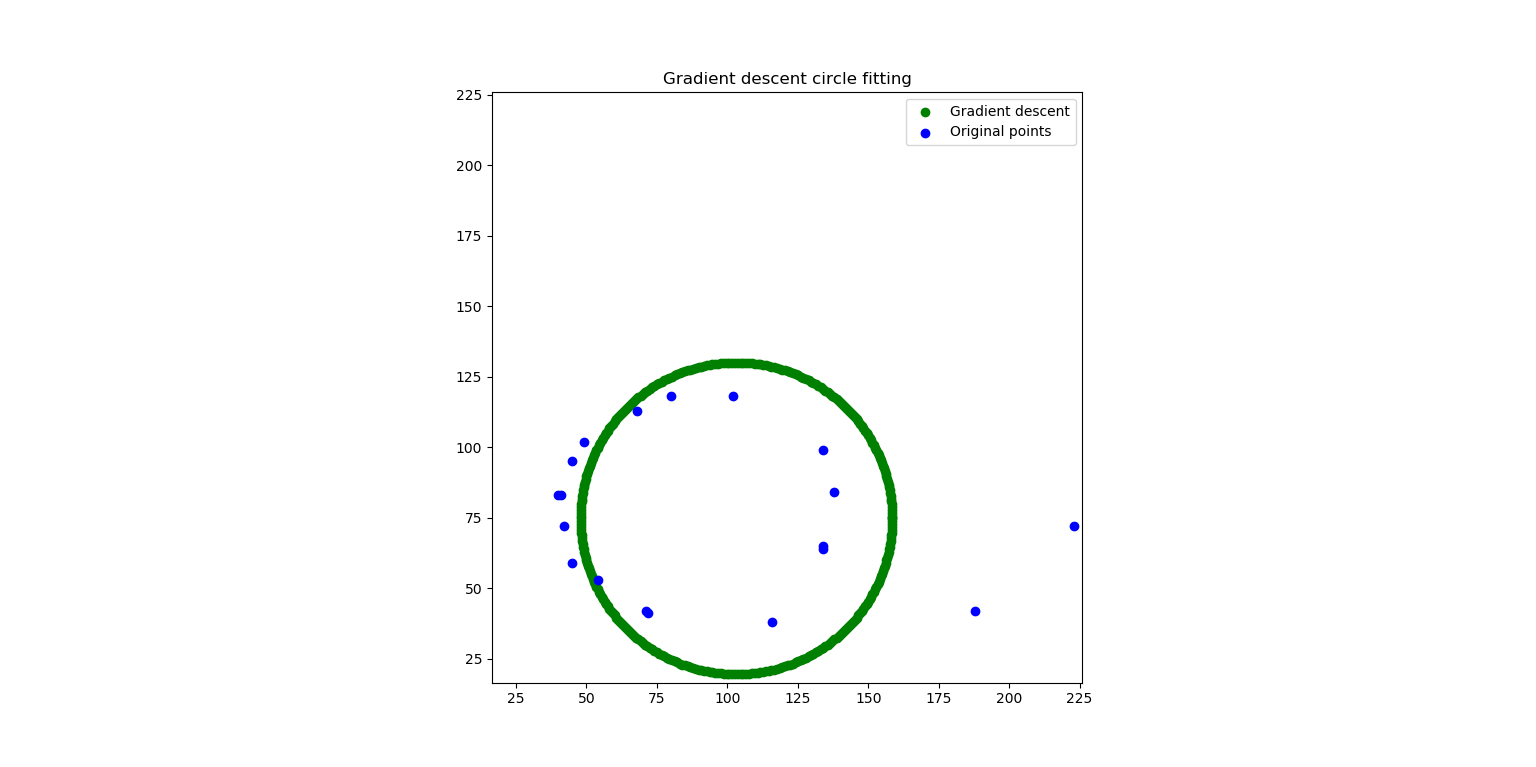
Fitting a circle - using Gradient descent algorithm

The output after finding the best fitting circle is presented below. Notice that the position of the circle has shifted towards the outliers

Fitting a circle - using RANSAC

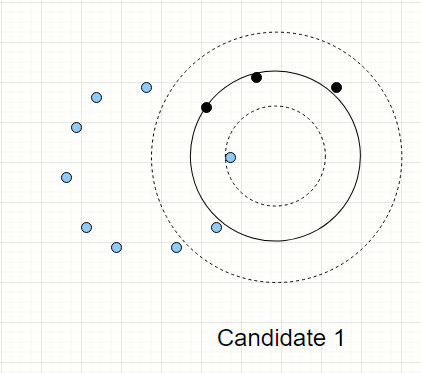
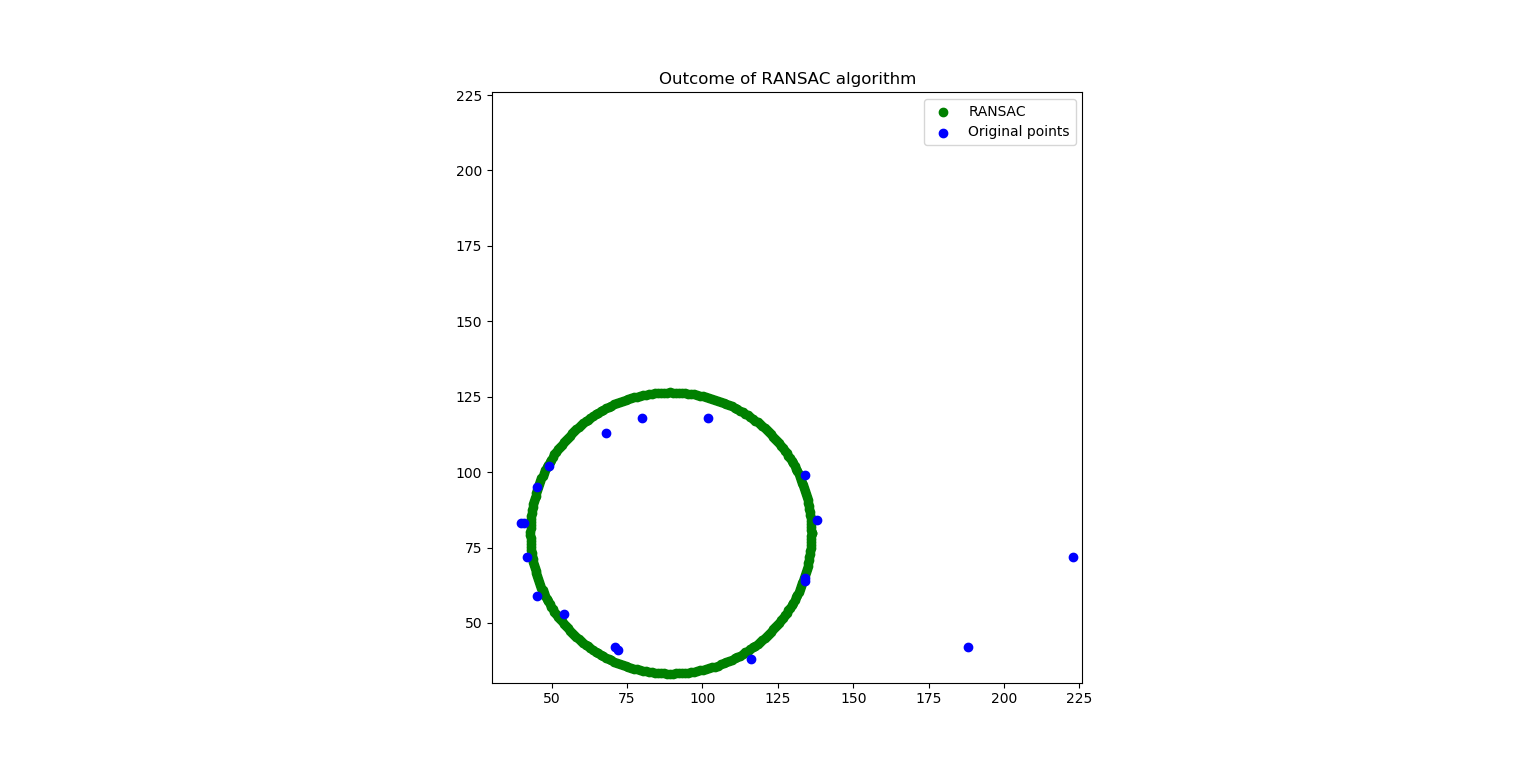
The output after using RANSAC to take into account the outliers. Notice that the algorithm has nicely detected the noisy points on the far right. The RANSAC algorithm has ignored the outliers completely.

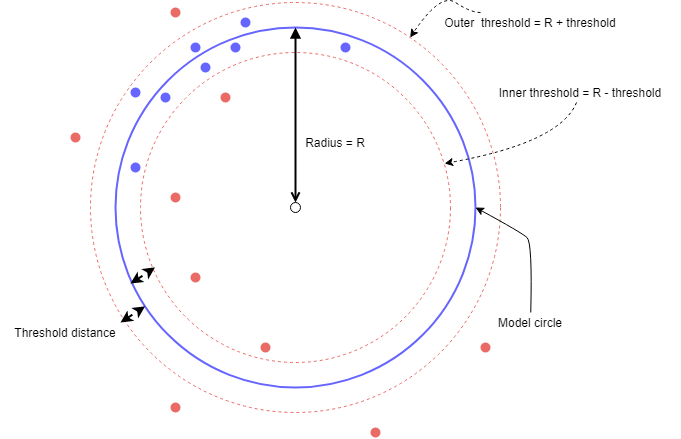
Understanding the RANSAC algorithm for fitting a circle

Key definitions

Model circle: The candidate circle which we think fits the points

Threshold distance: Used for creating a doughnut like concentric circles with the model circle in the middle

Outlier point: Any point outside the doughnut region

Inlier point: Any point within the doughnut region

Threshold inlier count: Minimum number of inliers points for a candidate circle to be selected

Mean absolute error: 1/N X Σabs(distance of inlier point from candidate center - radius of candidate center)
N=count of all inlier points

Initialize essential parameters

  1. Select a threshold distance - threshold distance
  2. Select a threshold count of inliners - threshold inlier count
  3. Select maximum number of samplings - max iterations

Build a shortlist of candidate circles

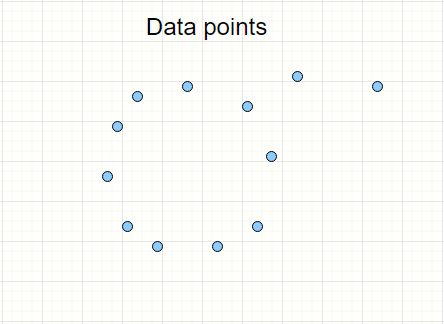
Consider the following arrangement of points. We will use this example for understanding the RANSAC algorithm

  1. Select any 3 points
  2. find the circle passing through these 3 points. This is our candidate circle.
  3. Use threshold distance and find all points which lie in the doughnut region. These are the inlier points.
  4. If the count is less than threshold inlier count then skip this candidate circle and go back to the first step.
  5. If the count exceeds threshold inlier count then move on to next step
  6. Use all inliner points and determine new candidate circle
  7. Find all new inliner points and new  outlier points for new candidate circle
  8. If the count of inlier points is less than threshold inlier count then skip this new candidate circle and go back to the first step.
  9. If the count exceeds threshold inlier count then move on to next step
  10. Calculate the mean absolute error for the new candidate circle using the new inlier points
  11. Add this candidate circle to the shortlist along with count of inlier points and the mean absolute error
  12. Go back to the first step and repeat for max iterations number of times
  13. When max iterations is completed, examine the shortlist of candidate circles and pick the circle with maximum inlier count. If more than candidate circles with same inliner count then pick the candidate circle with lesser mean absolute error

RANSAC examples

Example 1

Before

After


Example 2

Before

After


Example 3

Before

After


Example 4

Before

After


Example 5

Before

After


Why Gradient Descent?

RANSAC for straight lines relies on least squares algorithm to find the line which fits a set of points. When I started implementing RANSAC for circles, I was unsure of what would be the best mathematical approach to fit a circle to a set of points. Unlike the least squares method for lines, the equivalent approach for circles is non-linear and hard to solve without an interative approach I used the Gradient Descent Approach and this worked well. However, GD is an iterative approach and fairly expense. In the later stages I learnt of Randy Bullock's approach which reduces the non-learn optimization problem to a liner problem

Github

Link to source code

Github

About the source code

The folder hierarchy is as follows:

  1. Algorithm: Python classes which implement the actual RANSAC algorithms for line and circle
  2. Common: Python classes which implement common model classes like Circle,Line abd Util
  3. RANSAC: Scripts to launch the RANSAC algorithm using images in the 'input' sub-folder
  4. UnitTests: Unit tests for the algorithm classes

Quick start

You can chose either of the following:
  1. RANSAC\ExecRANSACCircle.py - Edit the .\input image filename in this script and execute. The output will be created in .\out folder
  2. UnitTests\ransac\test_RansaCircleHelper.py - You can debug the tests and do a walkthrough of the code